[논문 리뷰] Pyraformer: Low-Complexity Pyramidal Attention for Long-Range Time Series Modeling and Forecasting

Pyraformer: Low-Complexity Pyramidal Attention for Long-Range Time Series Modeling and Forecasting

https://openreview.net/forum?id=0EXmFzUn5I

Pyraformer: Low-Complexity Pyramidal Attention for Long-Range Time...

Shizhan Liu, Hang Yu , Cong Liao, Jianguo Li, Weiyao Lin, Alex X. Liu and Schahram Dustdar
ICLR 2022 (작성일 기준 인용 수: 984회)

 

요약

시계열 데이터의 특성을 올바르게 이해하기 위해선 multi-resolution representation을 파악할 필요가 있음
그렇기에 Pyramidal Attention Module을 활용해 최소한의 계산 비용으로 multi-resolution representation을 파악하고자 함

multi-resolution representation:
시계열 데이터를 단일 해상도(모든 데이터를 시간 단위로만 보는 방식)로만 보는 게 아니라, 여러 해상도(일별, 주별, 월별 등)으로도 나누어 표현하는 방법

 

Abstract

시계열 예측에서는 다양한 시간적 의존성을 포착할 수 있는 유연하면서 간결한 모델을 구축하는 것이 과제이다.
본 논문에서는 time-series의 multi-resolution representation을 탐구한 Pyraformer를 제안한다.

저자들은 피라미드형 어텐션 모듈(Pyramidal Attention Module, PAM)을 도입하였고,
여기서 inter-scale 트리 구조는 서로 다른 해상도의 특징을 요약하고 intra-scale neighboring connections는 다양한 범위의 시간 의존성을 모델링한다.

적절한 조건 하에서, Pyraformer의 최대 신호 경로 길이는 시계열 길이 $L$에 대해 상수( $O(1)$) 이며, 시간 및 공간 복잡도는 L에 대해 선형적으로 증가한다.

실험 결과는 Pyraformer가 single-step과 장기 multi-step 예측 작업에서 최고 예측 정확도를 달성하며 시계열이 길 때 메모리 소모가 가장 적음을 보여준다.

 

Introduction

기존 모델들이 시간 및 공간 복잡도를 크게 줄이는 모델이 없었기에 본 논문에서는 장기 의존성을 포착하고 낮은 시간 및 공간 복잡도를 달성하는 새로운 피라미드형 어텐션 Transformer 기반 모델인 Pyraformer를 제안한다.

그림1(d)에 있는 피라미드형 그래프에서 어텐션을 기반으로 메시지를 전달함으로써 피라미드형 어텐션 메커니즘을 개발했다.
이 그래프의 엣지는 두 그룹으로 나뉜다.
the inter-scale, the intra-scale connections.

inter-scale connection은 원래 시계열의 multi-resolution representation을 구축한다.
multi-resolution representation은 시계열 데이터를 단일 해상도(모든 데이터를 시간 단위로만 보는 방식)로만 보는 게 아니라, 여러 해상도(일별, 주별, 월별 등)으로도 나누어 표현하는 방법이다.
이러한 latent coarser-scale 노드는 CSCM(coarser-scale construction module)을 통해 구축된다.

반면 intra-scale 엣지는 각 해상도에서 이웃 노드를 연결하여 시간 의존성을 포착한다.

결과적으로 이 모델은 멀리 떨어진 위치 간의 장기 시간 의존성을 더 낮은 해상도에서 포착함으로써 신호 경로 길이를 줄이고, sparse neighboring intra-scale connections로 다양한 범위의 시간 의존성을 모델링하여 계산비용을 크게 줄인다.

 

Related Works

Time Series Forecasting: 통계적 방법은 장기 예측에 한계가 있고, 신경망 기반 방법은 복잡도와 경로 길이 간 트레이드오프가 존재

Sparse Transformers: NLP에서 Transformer의 효율성을 높이려는 시도가 있었지만, 여전히 경로 길이나 복잡도에 한계가 존재

Hierarchical Transformers: 계층 구조를 도입한 모델들이 있으나, 복잡도가 높음

Pyraformer는 mutil-resolution과 sparse attention을 결합해 기존 모델들의 단점을 극복하며, $O(L)$ 복잡도와 $O(1)$ 경로 길이를 동시에 달성한다.

 

Method

전체적인 모델 구조

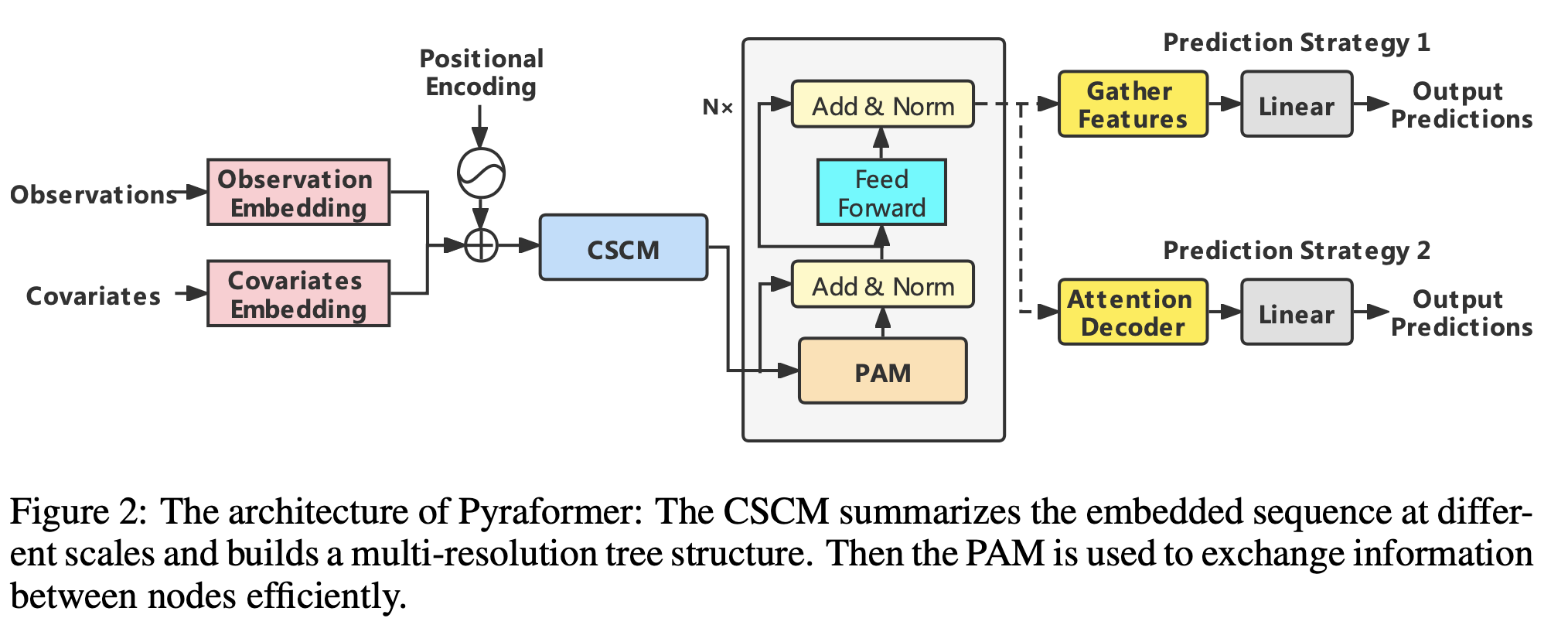
먼저 입력에서 observations, covariates를 각각 임베딩한 뒤 합친다.
이때 observations는 target feature를 의미하고, covariates는 나머지 설명 feature들을 의미한다.

그 뒤 positional encoding vector를 더해준다.
여기까지는 Informer와 동일한 방식이다.
다음으로 coarser-scale construction module(CSCM)을 사용하여 $C$-ary 트리를 구성한다.
도입한 Pyramidal Attention Module(PAM)에서 $C$-ary를 가지고 Attention을 진행한다.

그렇게 Encoder를 거치고 나면 마지막으로 하위 작업에 따라 다른 네트워크 구조를 사용하여 최종 예측을 출력한다.

자세한 내용은 아래에서 더 상세하게 설명하겠다.

 

Pyramodal Attention Module

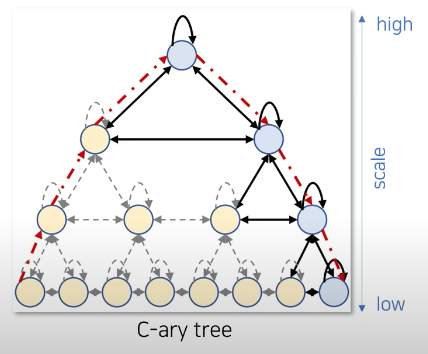
PAM은 피라미드형 그래프 구조를 활용하여 관측된 시간 시계열의 시간 의존성을 multi-resolution 방식으로 표현한다.
이는 시계열 데이터를 여러 층으로 나누어 표현하는 것과 같다.

예를 들어,

• 맨 위층(거친 스케일): 월 단위로 요약
• 중간층: 주 단위나 하루 단위로 요약된 데이터
• 맨 아래층(세밀한 스케일): 시간 또는 분 단위 데이터

이러한 multi-resolution 구조를 통해 단기패턴은 아래층에서, 장기 패턴은 위층에서 쉽게 분리해서 파악할 수 있다.

피라미드형 그래프는 두 가지 연결 방식을 가진다. inter-scale connection과 intra-scale connection
먼저 inter-scale connection은 아래 층과 위 층 간의 연결을 의미한다.
즉 finer 노드와 coarser 노드 간의 정보 교환을 진행하며

반대로 intra-scale connection은 이웃 노드 간, 즉 같은 sclae의 노드 간의 정보 교환을 진행한다.

그리고 Transformer에서는 장기 의존성을 모델링하기 위해 가장 fine한 스케일에서 모든 두 노드를 연결하는 풀 그래프를 채택하여, $O(L^2)$의 계산적으로 너무 높은 시간 및 공간 복잡도를 초래한다.
반면 피라미드형 그래프를 통해 위층에서 데이터를 요약하여 계산 비용을 $O(L)$로 줄일 수 있었다.

계산 비용을 줄이는 방법은 아래에서 자세하게 설명한다.

기존 transformer 방법은 모든 노드에서 다른 모든 노드를 확인한다.

여기서 $q_i$는 쿼리, $k_ℓ$는 키 $v_ℓ$는 값을 의미하며 L이 1000이라면 1000을 모두 확인해야한다.

반면 PAM의 어텐션 메커니즘은 연결된 이웃만 확인한다.
연결된 이웃 $\mathbb{N}_ℓ^{(s)}$은 같은 층의 이웃 A개 ($\mathbb{A}_ℓ^{(s)}$), 아래층의 자식 C개 ($\mathbb{C}_ℓ^{(s)}$), 위층의 부모 1개 ($\mathbb{P}_ℓ^{(s)}$) 가 있다.

이렇게 해서 아래의 수식은 최대 A + C + 1까지만 확인하면 되기 때문에 기존 방식보다 단축되게 된다.

논문에서 PAM의 장점은 2가지로 증명한다.

Proposition 1: 계산량
한 노드가 최대 $A + C + 1$개만 보기 때문에, 전체 계산량은 $O(AL)$이 된다.
여기서 $A$가 상수(ex: 3) 이면 $O(L)$로 줄어들게 된다.

Porosition 2: 경로 길이
두 노드 간 최단 경로가 짧다.
위 층으로 가면 멀리있는 데이터도 금방 연결되기 때문에 O(1)이 된다.

저자들은 실험에서 실제로 스케일 수 S와 N을 고정하고, A는 시퀀스 길이 L과 관계없이 3 또는 5만 사용했다.
따라서 제안된 PAM은 $O(L)$의 복잡도와 $O(1)$의 최대 경로 길이를 달성했다.

 

Coarser-Scale Construction Module (CSCM)

CSCM은 PAM에서 피라미드 구조를 가지게 하려면 먼저 데이터를 계층적으로 만들어야하는데 그 작업을 담당한다. 즉, 시계열 데이터를 세밀한 층과 거친 층으로 쌓아올리는 역할을 한다.

여기서 축약의 대상인 노드를 children, 축약된 결과 노드를 parent로 부른다.

자식 노드들을 가지고 convolution을 통해 parent로 만들게 되는데
stride 만큼의 자식 노드들로 convolution을 해서 parent를 만든다고 보면 된다.

CSCM의 구조는 아래와 같고 CSCM의 목표는 low scale의 노드들을 coarser하게 결합하여 high scale의 상위 노드를 만드는 것이라고 보면 된다.

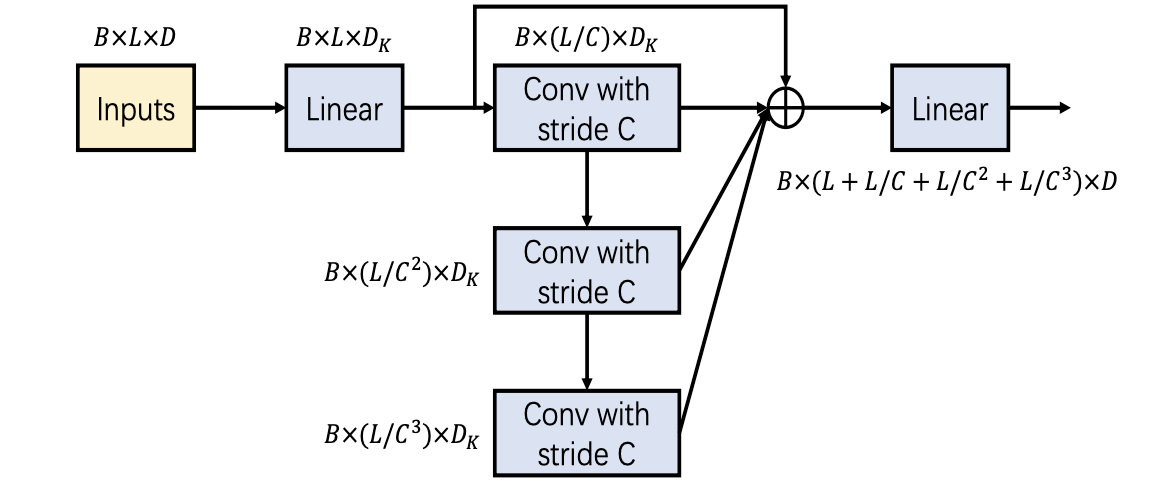
그래서 기본의 작은 스케일인 L 길이(sequence length)의 데이터들을 가지고 Convolution을 진행하여 큰 스케일의 데이터를 만들게 되는데 이때 사용되는 Convolution은 kernel size도 C이고 Stride도 C이다.
여기서 C는 한 번에 몇개 데이터를 묶을지 결정하는 값으로 층 별로 길이가 C배씩 줄어든다.

예를 들어 입력 L = 64이고 C가 4인 경우

첫 번째 Conv:
출력: 64/4 = 16개의 노드 (길이 $L/C$)
의미: 4일 단위로 요약된 데이터

두 번째 Conv:
출력: 16/4 = 4개 노드 (길이 $L/C^2$)
의미: 16일 단위로 요약된 데이터

세 번째 Conv:
출력:4/4 = 1개 노드 (길이 $L/C^3$)
의미: 64일, 즉 전체 요약 데이터

결과적으로 3개의 Conv layer에서 나온 출력은 각각 길이 16, 4, 1의 시퀀스를 의미하고 이게 $C$-ary 트리의 각 스케일에 해당하며 각 층의 출력을 시간 축에 따라 concat해준다.

그리고 앞과 뒤로 Linear layer가 존재하는데 이는 파라미터와 계산 효율을 위해 Convolution 이전에 차원을 축소하고, Convolution 이후 다시 차원을 복원하는 작업이다.

 

Prediction Module

Prediction Module은 Encoder를 거치고 나온 결과를 가지고 최종 예측을 내는 모듈이다.
여기에는 2가지 방법이 있고 내부에서 Single-step과 Multi-step으로 나뉜다.

Single-step Prediction: 미래의 한 시점만 예측 (ex: 다음날의 Close값)
Multi-step Prediction: 미래의 여러 시점을 한꺼번에 예측 (ex: 다음 7일 간의 Close값)

Prediction Strategy 1은 Single-step과 Multi-step 모두 가능하며
Prediction Strategy 2는 Multi-step만 가능하다.

Prediciton Strategy 1:
Single-step:
모델을 거치기 전에 과거 데이터의 마지막에 end token을 추가하여 모델에 입력한다. ($Z_{t+1} = 0$)
CSMS와 PAM을 거쳐 PAM representation이 완성되면 각 scale의 마지막 노드만을 concat하여 linear layer를 통과시켜 prediction을 수행한다.

Multi-step:
Single step과 동일하며 M개의 출력(ex: 7일치)를 한 번에 뽑는다는 점만 다르다.

Prediction Strategy 2:
이 방법에서는 transformer decoder처럼 2개의 full attention layer를 사용한다.
먼저 Encoder의 출력인 피라미드 그래프의 모든 스케일의 노드 정보 $F_e$를 미래 M개 시점 $F_p$로 임베딩한다.
decoder layer 1: $F_p$를 Query로, Encoder의 output인 $F_e$를 key, value로 하여 $F_{d1}$을 얻는다.
decoder layer 2: $F_{d1}$을 Query로, $F_{d1}$과 $F_e$를 concat한 걸 key, value로 하여 output을 산출한다.
이 output을 linear layer를 통과시켜 최종 prediction을 얻는다.

두 번째 방법은 FC layer로 한 번에 예측하는 것보다 full attention을 두 번 거침으로 더 깊이 분석할 수 있으며 장기 예측에서 더 정확하다.
그리고 이름을 Decoder라고 붙이긴 했지만 auto regressive 하게 진행하지는 않고 한 번에 출력을 내게 된다.

공식 코드를 확인했을 때 방법 1을 사용한 것으로 보이고 time series library에는 방법 1으로만 구현되어있다.

 

Experiments

Single-step forecasting results on three datasets

Q-K pairs는 네트워크 상에서 계산되는 모든 query-key dot product의 수를 의미한다.
모든 데이터셋에 대해 Pyraformer가 가장 좋은 성능을 보였으며 Q-K pairs 또한 가장 낮은 것을 볼 수 있다.
full attention과 Pyraformer의 Q-K pairs를 비교해보면 20배 가량 차이가 존재한다는 점도 눈에 띈다.

 

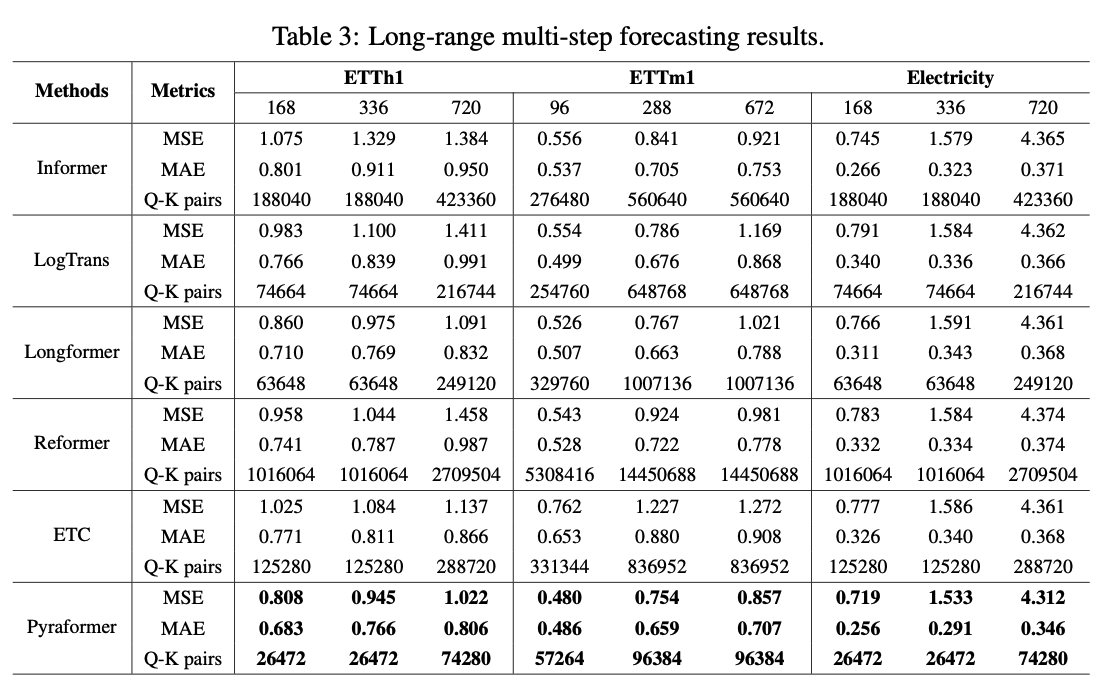
이것 또한 모든 데이터셋에 대해 Pyraformer가 가장 좋은 성능을 보였으며 Q-K pairs 수도 확실히 낮은 것을 확인할 수 있다.

 

Comparison of the time and memory consumption

실제로 시간과 계산량이 줄어들었음을 시각화한 내용이다.

full attention
sparse attention
TVM으로 구현한 Pyraformer

왼쪽 그래프는 sequence 길이가 증가함에 따라 배치 별 계산에 걸리는 시간을 시각화하였고
오른쪽 그래프는 sequence 길이가 증가함에 따라 차지하는 메모리양을 시각화한 결과이다.

 

Conclusion

본 논문은 낮은 시공간 복잡도만으로 short & long temporal dependencies를 잘 포착할 수 있는 Pyramidal attnetion 구조를 제안하였고 논문에서 제안한 CSCM layer, PAM, Prediction Module을 활용해 Single-step, Multi-step Forecasting 모두에서 낮은 계산 복잡도로 S.O.T.A 성능을 달성하였다.

 

참고자료

공식코드
https://github.com/ant-research/Pyraformer

GitHub - ant-research/Pyraformer

 

시계열 예측이란?
https://bo1126.tistory.com/20

Time-Series Forecasting(시계열 예측)이란?

 

시계열 예측 논문에서 자주 사용하는 기본 Notation 정리
https://bo1126.tistory.com/22

시계열 예측 논문에서 자주 사용하는 기본 Notation 정리

---

해당 모델은 나온지 오래된 모델이다보니 벤치마크에서도 현재 낮은 성능을 가진 모델이며
직접 주기성이 적은 주식 데이터로 실험을 진행해본 결과 굉장히 낮은 성능을 보였습니다.

하지만 참신한 구조로 시간복잡도를 낮추고 다양한 방법을 간단하게 설명한 좋은 논문이라고 생각합니다.

되도록이면 논문리뷰에 의존하기보단 참고용으로만 사용하시고 논문을 직접 보길 권장드리며
혹시라도 글에 잘못된 부분이나 피드백, 또는 궁금한 사항이 있으시다면 편하게 댓글 남겨주시면 되겠습니다.